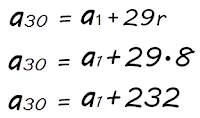Vamos demonstrar como se calcula a Soma dos n primeiros termos de uma progressão
aritmética (PA)
Considere a PA com os seguintes termos (2, 6, 10,
14, 18, 22), vamos somar todos esses termos
Esse é um modo muito trabalhoso, pois se temos uma
PA com um número de termos grande, precisamos saber todos e depois
soma todos eles, porém a matemática desenvolveu um modo bem mais simples, e vamos
demonstrar logo abaixo.
De modo geral, para se calcular a soma dos n termos de uma PA, usamos a fórmula abaixo
Vejamos alguns exemplos:
- Determine a soma dos termos da PA (-10, -5, 0, ... ,75)
O primeiro termo dessa PA é -10, o último é 75 e a sua razão é
5, pela fórmula mostrada acima, não precisamos da razão para calcular a
soma dos termos, mas não temos o número de termos, e por esse motivo a
razão será necessária.
Então vamos começar utilizando o termo geral da PA para calcular o número de termos.
Agora, que já temos o número de termos, já podemos utilizar a fórmula para determinar a soma dos termos.
Então, essa PA tem 585 como soma de todos os seus termos.
2.
A soma dos 30 primeiros termos de uma PA é 420,
sabendo que a razão é 8, que
valor representa o 16° termo dessa PA?
Para determinar o 16° termo, basta fazer a16 = a1 + 15r, como
a razão já está determinada na questão, precisamos encontrar o 1º termo.
Então vamos definir o 30º termo em função do 1º.
Então vamos definir o 30º termo em função do 1º.
Usando a soma dos termos, vamos encontrar o que estamos procurando (1° termo).
Agora basta substituir a1 por -74 e r por 8
O 16º termo dessa PA é 46.